2.2. The non-linear form of the interference field
2.2. The non-linear form of the interference field |
|
Until recently it has been assumed that the shape of the interference field is "linear".
The corresponding fraction of the shift of the interference fringes is directly proportional to the
corresponding part of the wave length. If, for example, the distance of two interference fringes is
divided into 100 divisions and the shift of 23 divisions is detected, we thus assume that the change occured
over a length of 
.
In other words, the shift of the fringes is considered to be equivalent to the change of length. This view corresponds to the linear form of the interference field, see fig. 2.12.
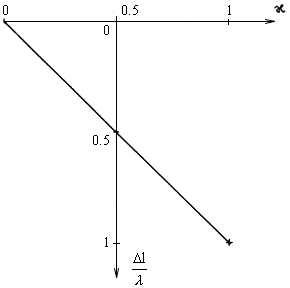
Fig. 2.12. The "linear" form of the interference field
What justifies us our assumption that the interference field is linear? Is the assumption correct?
In physics we are used to picture the experimental results through curves which are not "saw-tooth" as is the case with the linear interference field, but which have a nicely rounded shape. Let us replace the "saw-tooth" linear interference field by some rounded non-linear interference field.
Let us choose sinusoides or semi-circles instead of the sawtooth abscissas. In case of semi-circles according to fig. 2.13 we get:
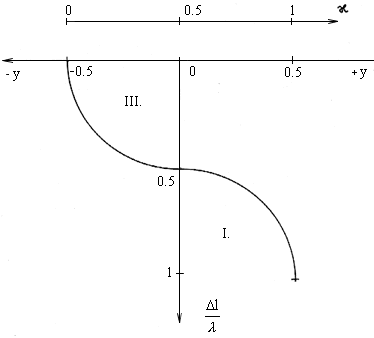
Fig. 2.13. The non-linear form of the interference field
in the 3rd quadrant: 
, as
 |
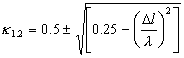(2.46) |
 |
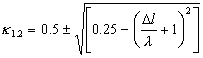(2.47) |
Let us revalue the results of the Fizeau's experiment from the aspect of non-linear interference
field. Fizeau [3] used light of wave length
, two tubes, each L=1.4875 m
long in which water flowed at speed u=7.059 m/s. As the experiment is generally known, we shall
not describe it in detail. We shall only reassess its results.
The relation 
corresponds to equal values
of the shift of fringe 
supposing the interference
field to be linear. In reality the experimentally observed values from the interval ranged from 0.167
to 0.307 in the average of 
. That was explained
by Fresnel's theory of partial drag of ether with the drag coefficient 
.
Should we consider the non-linear form of the interference field, then according to (2.46)
we get
which is in line with the experimentally
observed mean value 
. We do not need any coefficient
. Fizeau's experiment confirms also that the interference
field has a non-linear form.
Harres [4] used two wavelengths of light
which were passing through ten firmly fastened prisms in a rotating apparatus at speed 400-600 revolutions/min.
According to [4], if the drag coefficient
is not included
were 
, z - is the number of sideral time seconds
required by the apparatus to make 50 revolutions.
After the arrangement
 |
(2.48) |
 |
(2.49) |
(tab. 1) after substitution in (2.48) gives
Substituing 
to (2.46)
we get
According to the experiment 
is again in line with the theory of the non-linear
interference field. The comparison of Harres's experimental values that do not include the drag coefficient
with both linear and non-linear form of the interference field, as well as the results of Fizeau's experiment, are shown in figs.
(2.14)-(2.21).
Fig. 2.14.-2.21. The comparison of Harre's experimental values which do not comprise the drag coefficient with both linear and non-linear form of the interference field, as well as the results of Fizeau's experiment.
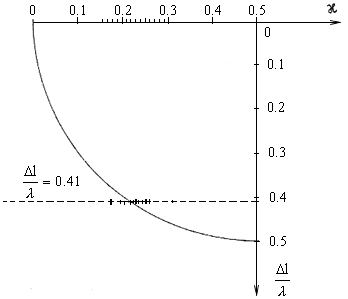
Fig. 2.14. Fizeau's experiment [3] p. 392
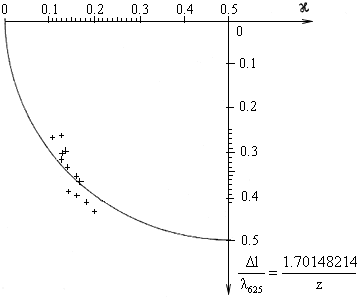
Fig. 2.15. [4] Tab. 1., 1. Reihe
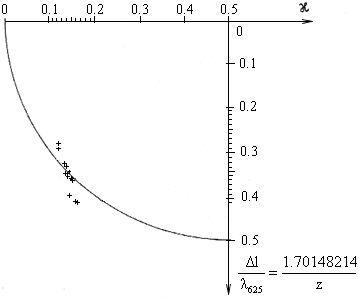
Fig. 2.16. [4] Tab. 1., 2. Reihe
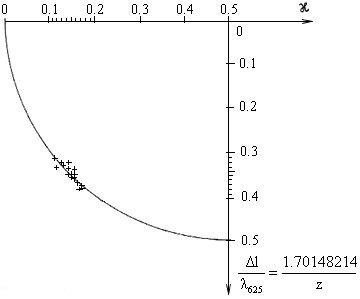
Fig. 2.17. [4] Tab. 1., 3. Reihe
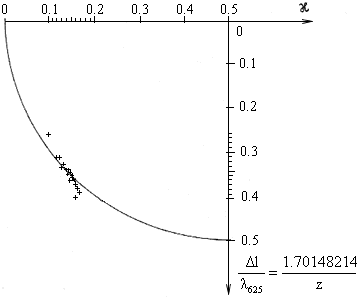
Fig. 2.18. [4] Tab. 1., 4. Reihe
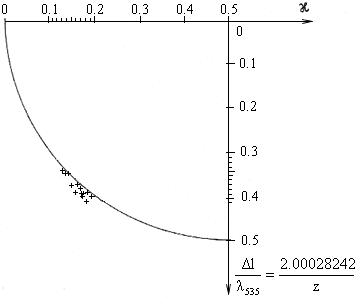
Fig. 2.19. [4] Tab. 2., 1. Reihe
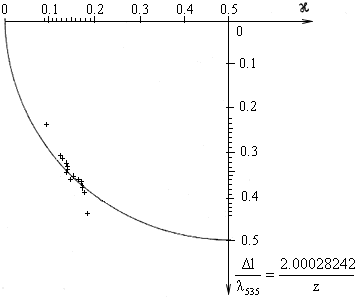
Fig. 2.20. [4] Tab. 2., 2. Reihe
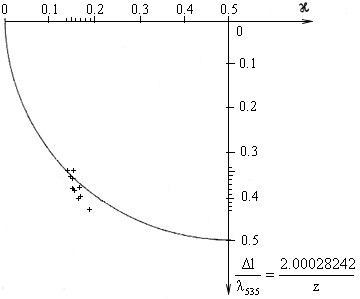
Fig. 2.21. [4] Tab. 2., 3. Reihe
This is simultaneously proves that the drag coefficient always equals one and the interference field has a non-linear form. Consequently, the interference fields are identical only for the shift of the interference fringes about 0 and/or 100 and 50 divisions.
|
|